Tiga Sifat Perpangkatan terkait Perkalian

KITA telah belajar tentang definisi dan sifat-sifat dari bilangan berpangkat. Pada pelajaran matematika di Kelas IX SMP (sekolah menengah pertama), kita akan belajar tentang sifat-sifat dari perpangkatan, terutama dalam soal perkalian.

Eksis tiga bentuk sifat terkait perkalian dalam perpangkatan yang mesti dipelajari dan dipahami. Tiga sifat tersebut ialah mengalikan dua perpangkatan dengan basis yang sama, hasil pemangkatan dari perpangkatan dengan basis yang sama, dan hasil perpangkatan dari suatu perkalian bilangan.

Bagaimana penjelasan tentang tiga sifat terkait perkalian dalam perpangkatan? Kepada lebih Jernih berikut uraiannya yang dilansir dari Naskah Matematika Kepada SMP/MTs Kelas IX dengan penulis Subchan dkk.

Baca juga : Bilangan Berpangkat: Definisi dan Teladan Soal

1. Sifat perkalian perpangkatan dengan basis yang sama.

Sifat perkalian dalam perpangkatan dirumuskan sebagai berikut.

  a^m × aⁿ = a^{m + n}

Teladan:

a. 3² × 3³ = 3^{2 + 3} = 3⁵ = 243

b. 4³ × 4² = 4^{3 + 2} = 4⁵ = 1024

Baca juga : Konfigurasi Elektron Tentukan Metode Atom-Atom Berikatan

c. (–4)² × (–4)³ = = (–4)^{2 + 3} = (–4)⁵ = –1024

d. m³ × m⁵ = m^{3 + 5} = m⁸

Agar lebih paham, kita dapat pelajari tabel berikut. Tipe soal sejenis dengan Metode mengerjakan berbeda tetapi tetap menghasilkan yang Benar.

Baca juga : Perkembangan Lima Teori Atom oleh para Ilmuwan

2. Sifat pemangkatan dari perpangkatan dengan basis yang sama.

Sifat pemangkatan pada perpangkatan dirumuskan dalam bentuk berikut.

  (a^m)ⁿ = a^{m ∙ n} = a^mn

Teladan

a. (3²)³ = 3^2∙3 = 3⁶ = 729

Baca juga : Tiga Metode Hewan Berkembang Biak: Ovipar, Vivipar, dan Ovovivipar

b. (4³)² = 4³ × 4³

             = 4^{3 + 3}

             = 4⁶ 

            = 4096

b. (x³)⁴ = x³ . x³ . x³ . x³

             = x^{3 + 3 + 3 + 3}

             = x¹²

Agar lebih paham, kita dapat pelajari tabel berikut. Tipe soal sejenis dengan Metode mengerjakan berbeda tetapi tetap menghasilkan yang Benar. 

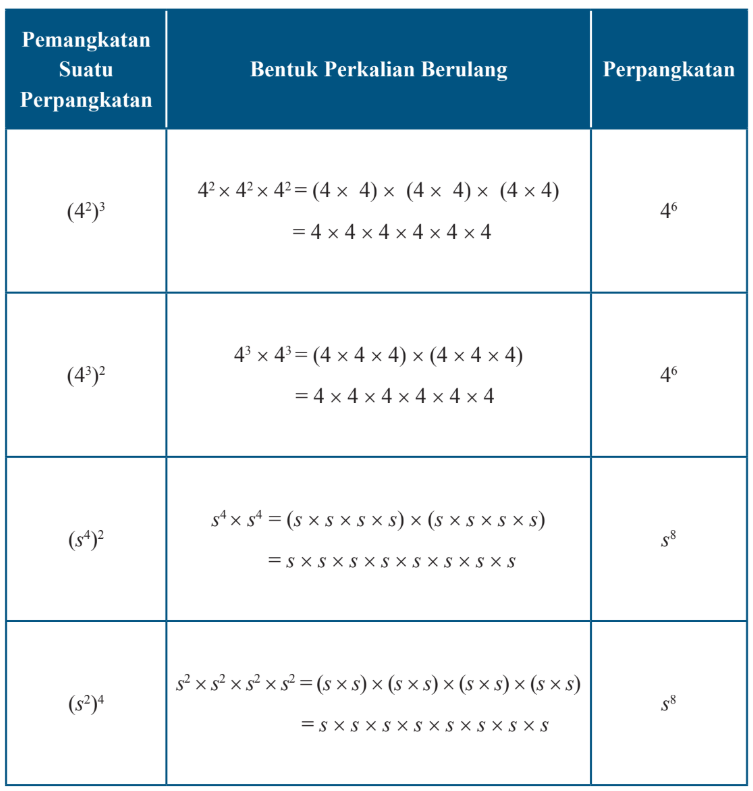
3. Sifat perpangkatan dari suatu perkalian bilangan.

Sifat perpangkatan dari perkalian bilangan dirumuskan dalam bentuk berikut.

(a∙b)^m = a^mb^m

Teladan:

a. (2∙3)³ = 2³∙3³

b. (4y)² = 4y × 4y

= (4 × 4) × (y × y)

= 4² × y²

= 16y²

c. (wy)³ = wy × wy × wy

              = (w × w × w) × (y × y × y)

              = w³y³

Agar lebih paham, kita dapat pelajari tabel berikut. Tipe soal sejenis dengan Metode mengerjakan berbeda tetapi tetap menghasilkan yang Benar.

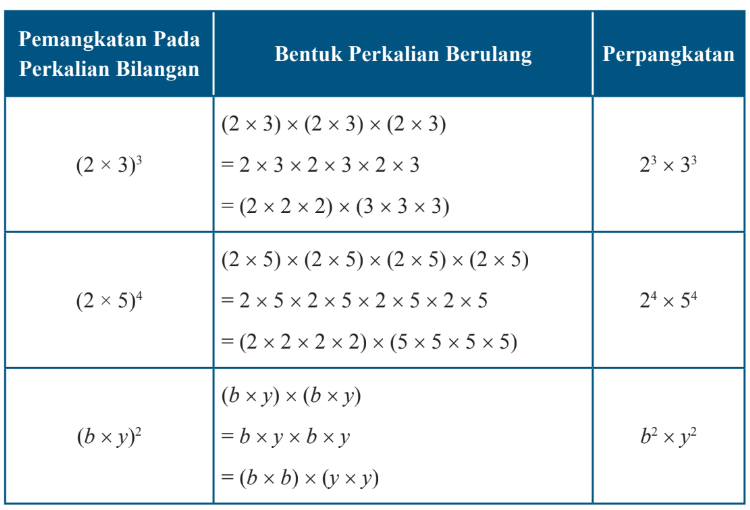
Itulah tiga sifat perpangkatan yang terkait dengan perkalian. Setelah ini, kita akan belajar sifat perpangkatan terkait operasi pembagian. Semangat belajar. (Z-2)